Круги Эйлера, на самом деле, достаточно часто встречаются в нашей жизни. Еще в младшей школе ученики начинают работать со схематическими фигурами, которые наглядно объясняют соотношения предметов и понятий.
Описание схемы кругов Эйлера
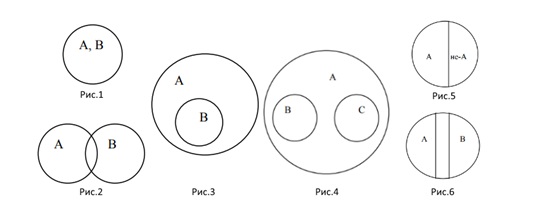
Круги Эйлера – геометрические конструкции, применяемые для упрощения восприятия логических связей между предметами, понятиями и явлениями.
Делятся на группы, в зависимости от типа отношений между множествами:
- равнозначные (рис.1);
- пересекающиеся (рис.2);
- подчиненные (рис.3);
- соподчиненные (рис.4);
- противоречащие (рис.5);
- противоположные (рис.6).
Типовой пример такой диаграммы:
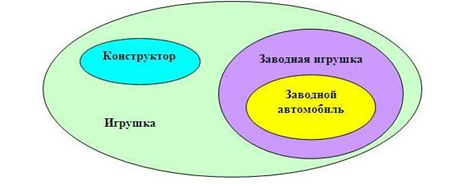
Наибольшее множество, отмеченное зеленым цветом, представляет собой все варианты игрушек.
Одним из вариантов игрушек являются конструкторы. Они выделены голубым овалом. Конструкторы являются отдельным множеством, и, одновременно, частью множества «Игрушки».
Заводные игрушки также являются частью множества «Игрушки», но не относятся к множеству «Конструкторы». Поэтому, они выделяются фиолетовым овалом. А вот множество «Заводных автомобилей» является самостоятельным, но при этом, является подмножеством «Заводных игрушек».
При помощи этого метода ученый решал сложнейшие математические задачи. Применение простых фигур позволяло свести решение любой, даже самой сложной задачи, к символической логике – максимальному упрощению рассуждений.
Позже, данный способ был доработан англичанином Джоном Венном, который ввел понятие пересечения нескольких множеств.
Методика очень проста в использовании — круги Эйлера для дошкольников от 4-5 лет начинают преподавать уже в детском саду. При этом, она же на столько удобна, что применяется даже в высшей академической среде.
Применение кругов Эйлера
Основная цель использования диаграмм – практическое решение задач по объединению или пересечению множеств.
Области применения: математика, логика, менеджмент, статистика, информатика и др. На самом деле, их значительно больше, но перечислить все попросту невозможно.
Диаграммы делятся на два вида.
Первый описывает объединение понятий, вложенность одного в другое. Пример приведен в статье выше.
Второй описывает пересечения двух разных множеств некоторыми общими признаками. Один из примеров
Примеры задач и решения
Рассмотрим задачи, в которых помогают разбираться круги Эйлера, примеры решения задач по логике и математике.
Задачи для дошкольников

Первые в очереди: круги Эйлера для дошкольников, задания с ответами на которые помогут понять, как малыши впервые знакомятся с методикой упрощения сложных математических и логических задач.
Задание №1 – начальный уровень.
Цель: научить ребенка определять предмет, наиболее соответствующий одновременно двум свойствам.

Правильный ответ: кубик Рубика.
Задание №2

Правильный ответ: лягушка.
Задание №3

Правильный ответ: груша.
Задание №4 – средний уровень.
Задания усложняются тем, что используется больше множеств.

Правильный ответ: Солнце.
Задание №5

Правильный ответ: платье.
Задание №6
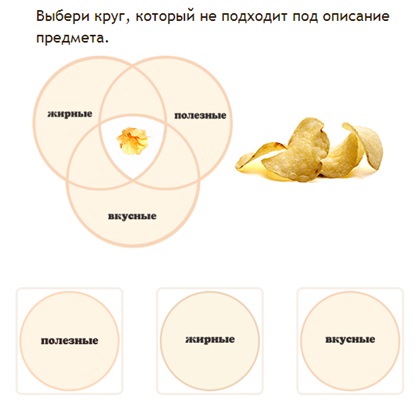
Правильный ответ: полезные.
Задания для школьников
Следующие задачи по логике с ответами, круги Эйлера в которых являются основой для решения, касаются младших школьников. Подобные задания обучают детей разбирать логические пересечения по определенным признакам.
Задание №1
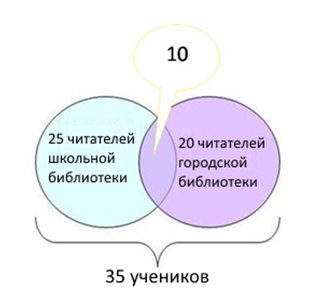
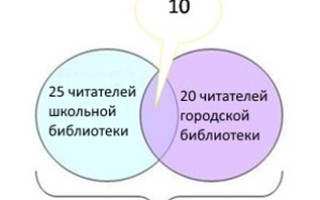
35 учеников зарегистрированы в школьной или городской библиотеках. Из них 25 регулярно посещают школьную библиотеку, а 20 – городскую.
Сколько учеников:
- Посещают обе библиотеки?
- Не посещают городскую библиотеку?
- Не посещают школьную библиотеку?
- Ходят только в городскую библиотеку?
- Ходят только в школьную библиотеку?
Ответ:
- Определим количество посетителей двух библиотек – общая часть на диаграмме:
(25 + 20) – 35 = 10.
- Ученики, не посещающие городскую библиотеку:
35 – 20 = 15 – левая сектор голубой зоны.
- Ученики, не посещающие школьную библиотеку:
35 – 25 = 10 – правый сектор фиолетовой.
- Посетители только городской библиотеки:
35 – 25 = 10 – также, правый сектор фиолетовой.
- Посетители только школьной библиотеки:
35 – 20 = 15 – также, левый сектор голубой.
Задание №2 – также предназначено для младших классов, но является более сложным.

В 7-А учится 38 человек. Ученики увлекаются разными спортивными играми: 16 – баскетболом, 17 – хоккеем, 18 – футболом. Одновременно баскетбол и хоккей любят 4 человека, баскетбол и футбол – 3, хоккей и футбол – 5, а 3 ученика не интересуются спортом.
Вопрос:
- Есть ли ученики, увлекающиеся всеми спортивными играми?
- Какое количество школьников интересуется только одной из спортивных игр?
Ответ:
Все ученики класса – наибольшая окружность.
Круг «Б» — баскетболисты, «Х» — хоккеисты, «Ф» — футболисты, «Z» — универсальные спортсмены. Трое неспортивных учеников просто находятся в общем круге.
Баскетболисты, входящие в множество «Б», но не входящие в зоны пересечения со множествами «Х» и «Ф».
16 – (4 + Z + 3) = 9 – Z.
По аналогии, находим количество хоккеистов.
17 – (4 + Z + 5) = 8 – Z.
Футболисты.
18 – (3 + Z + 5) = 10 – Z.
Чтобы пределить значение Z, нужно суммировать множества учеников.
3 + (9 – Z) + (8 – Z) + (10 – Z) + 3 + 4 + 5 + Z = 38;
42 – 2*Z = 38;
Z = 2.
Соответственно, Б = 7, Ф = 8, Х = 6.
Применение круговых диаграмм позволяет наглядно продемонстрировать все взаимоотношения разных групп учеников.
Метод схематического изображения взаимоотношений множеств – не просто увлекательная вещь. Круги Эйлера, примеры решения задач, логика которых неочевидна, показывают, что метод может использоваться не только при развязывании математических заданий, но и находить выход из житейских ситуаций.




 (27 оценок, среднее: 3,74 из 5)
(27 оценок, среднее: 3,74 из 5)